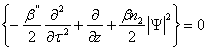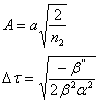1 ����`���w���ۂƔ���`�t�@�C�o
1.1 ���`���w�Ɣ���`���w
�ψ�Ȕ}���ɂ����āC���r�[���̓`�����x���́C����}���̋��ܗ��C����^�ł̌����x�Ƃ���ƁCv=c/n�ŗ^������D2�̈قȂ�}���ɂ����ẮC�U�d���̕s�A�����̂��߂ɔ��˂Ƌ��܂��N����D
�}���̋��ܗ��͈�ʂɌ��q�̍\����d�q�̕��z�Ɉˑ�����D����}���ɏƎ˂���ƁC�d���͌��r�[���̓d��ɂ��U�����C���˓d��ɔ�Ⴕ���d���g��������D���̎��}����`������d��ɂ͈ʑ��̂��ꂪ�����C�}�����̈ʑ����x���^�ɔ�ׂĒx���Ȃ�D�������˃r�[���̋��x���������Č��d�ꂪ���q�̓����d��ɔ�ׂď\�����������ɂ́C���̈ʑ�����͌����x�Ɉˑ����Ȃ��D���Ȃ킿���ܗ��͌��r�[�����x�Ɉˑ����Ȃ��D�ȏ�̏ꍇ����`���w�̗̈�ƌ����D
���d��̑傫�����}�����q�̓����d��ɋ߂��Ȃ�ƁC�}�����ł̓d�q�̕��z�����ˌ��d��ɂ��ω�����悤�ɂȂ�C�}���̋��ܗ��͐��`�Ȍ��w�����̎��Ƃ͈قȂ������̂ƂȂ�D�����Ȃ�Ƌ��E�ʂł̔��ˁE���܂�}�����̓`���̗l�q�͓��ˌ����x�Ɉˑ����邱�ƂɂȂ�D��������`���w�̗̈�ƌ����D
����`�ƌĂ�闝�R�́C�}�������d��̐U���ɑ��Ĕ���`�ȉ������������Ƃɂ��D����`�̗̈�ɂ����āC�}�����̌��r�[���̓`����Ԃ́C���ܗ��Ɉˑ�����D���̋��ܗ������r�[���ɂ���Đ���ł���̂Ȃ�C���r�[����葼�̌��r�[���̓`����Ԃ𑀍삷�邱�Ƃ��ł��邱�ƂɂȂ�D���̂悤�ɁC����`���w�͌��E��������\�Ƃ��C���ʂȋZ�p�v�V�̉\�����߂���ƌ����C�������̌������Ȃ���Ă���D
1.2�@����`���w����
���̓d���g���_�ɂ��ƁC�}���̌��d��ɑ��鉞���͎����̂悤�ɋL�q�����D
P=��0x(1)E+��0x(2)EE+��0x(3)EEE+��� (1)
P�F�}���ɗU�N����镪�Ɂ@�@![]() �F�^��̗U�d��
�F�^��̗U�d��
E:���d��@�@x(1)�Cx(2)�Cx(3)�F�萔
���`���w�̗̈�ɂ�����x(1)�́C���ܗ�n��
n2=1+x(1) (2)
�Ȃ�W�Ō���Ă���D�}����x(2)��x(3)�ɂ�����`���w�����������Â�����D�������C������x�ł́C�����̍��̒l�����ɏ������C��1����0x(1)E�݂̂Ō��w���ۂ��悭�������邱�Ƃ��ł���(����`���̉e����������)�D���Ĕ���`���w�̗̈�ɂ����āC(����`)�}���̋��ܗ���
n=n0+n2I (3)
�̂悤�ɋL�q�����D�����ŁCn1 n2�͒萔�CI�͌����x�ł���D�萔n2�̓J�[�iKerr�j�W���ƌĂ��W���ł���D���t�@�C�o�ޗ��ł�����w�K���X�̃J�[�W��n2��3.2�~10-16cm2/W�ƂȂ�D
�@���ɂ�����2���̍�[��0x(2)EE]�͑�2�����g�����i���g�����{�j�C�a�E�����g�������C�p�����g���b�N�����E���U�Ȃǂ́C3���̍�[��0x(3)EEE]�͑�3�����g�����CRaman�U���CBrillouin�U���C���Ȏ����iself-focusing�j�C���ʑ������Ȃǂ̗l�X�Ȕ���`���w���ۂ��錴���ƂȂ�D
1.3 ����`�t�@�C�o
�`���H�p�t�@�C�o���Ő�����Raman�U����Brillouin�U���Ȃǂ̔���`���ۂ�,�m�C�Y�̔�����g�`�̘c�݂ƂȂ��ĐM��������錴���ƂȂ�D���̂��ߓ`���Ɨp�t�@�C�o�ɂ����Ă͂ł��邾������`�������N�����ɂ������邱�Ƃ��]�܂�Ă���D�������C����Ŕ���`���ۂł���l���g�����⎩�Ȉʑ��ϒ���ϋɓI�ɗ��p���邱�Ƃɂ��C�����̔g���̐M�������ꊇ���Ĕg���ϊ����邱�Ƃ�C�p���X�̈��k�C�\���g��[*]�`�����\�ł��邱�Ƃ���������Ă���D
���t�@�C�o���Ő��������`���w���ʂƂ��ẮC���Ȉʑ��ϒ��iSPM�j�C���݈ʑ��ϒ��iXPM�j�C�l���g�����iFWM�jRaman�U���EBrillouin�U��������������D���Ȉʑ��ϒ��́C�P�Ƃňʑ��V�t�g���錻�ۂł���C���݈ʑ��ϒ��́C�g���̈قȂ���������������ɓ`������Ƃ�������ʑ��̃V�t�g���ۂł���D���Ȉʑ��ϒ��𗘗p���ăp���X�̈��k��\���g���`�����\�ƂȂ�D�܂��C�l���g�����𗘗p���Ĕg���̕ϊ����\�ƂȂ�D�����Ŏ��͈ȍ~�ł͔���`�t�@�C�o���ł̔���`�̗��p�Ƃ��āC�g���̕ϊ��ƁC�p���X���k�E�\���g���`���ɂ��Đ�������D
2 �l���g�����Ɣg���ϊ�
�l���g�����iFWM, Four-WaveMixing�j�͌��J�[���ʂ̈��ł���C��ȏ�̈قȂ����g���̌����t�@�C�o���ɓ��˂����ۂɐ�����DFWM�͈�ʂɂ͎O�̈قȂ����g���̌������t�@�C�o���ɓ��˂����ۂɁC�����̂ǂ̔g���Ƃ���v���Ȃ��g���ɐV���Ɍ����������錻�ۂł���D�����������̓A�C�h���iidler�j���ƌĂ��D
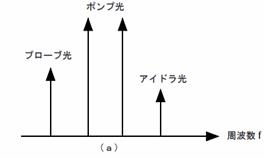
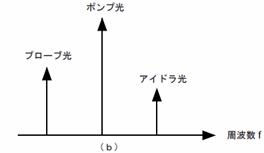
�@FWM�̔����̊T�O�}��}�P�Ɏ����D
�}
1�@���g����ɂ�����l���g�����̊T�O�}
(a)�|���v�����Q�g�̏ꍇ
(b)�|���v�����P�g�̏ꍇ�i�k�ގl���g�����j
�}1�Ɏ������悤�ɁC���g�������2�̃|���v�����Ԃɂ͂���ŁC���ˑO���炠�������͐M�����i���̓v���[�u���j�Ƃ���D�v���[�u���̎��g����fprobe�|���v���̎��g�������̂���fp1�Cfp2�Ƃ����ۂɁC�A�C�h�����̎��g����
fidler = fp1 + fp2
– fprobe (4)
�ƂȂ�D���̏����͎��g���̈ʑ����������ƌĂ��D�Ƃ���2�̃|���v���̎��g�����������ꍇ�C�k�ގl���g�����iDFWM�CDegenerated Four-Wave Mixing�j�ƌĂ��D���̂Ƃ����C�͎����̂悤�Ɏ������D
Fidler = 2fp – fprobe (5)
������fp�͏k�ނ����|���v���̎��g���ł���D�A�����ł�DFWM�͈ȉ��̂R���A������`������������ŋL�q�����D
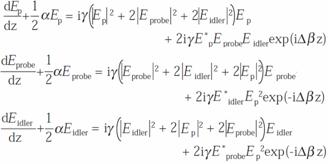 (8)
(8)
������z�̓t�@�C�o�̒�������ɂ킽����W������킷�D���͌��t�@�C�o�̌����W���CEp�CEplobe�CEidler�͂��̂��̂̃|���v���C�v���[�u������уA�C�h�����̓d���\���D���͒f�ʐςƔ���`���ܗ���苁�܂����`�W���ł���C�ȉ��̂悤�ɗ^������D
![]()
![]() (7)
(7)
n2�͔���`���ܗ��ł���CAeff�͗L���R�A�f�ʐςł���D���͐^�̌��̑�����\���D���@�Ɍ���������͓`���萔�̈ʑ��s������\���C�ȉ��̂悤�ɋL�q�����D
![]() (8)
(8)
D�͔g�����U�W���ł���D���t�@�C�o���ł��������O�̂Ƃ��ł������悭FWM����������D���̂��߂Ɍ����̗ǂ�FWM�������邽�߂ɂ́C�땪�U�g�����ł��邾����v�����邱�Ƃ��v�������D�������̑�1���ڂ͌��J�[���ʂɂ�鎩�Ȉʑ��ϒ�����ё��݈ʑ��ϒ��̌��ʂ�\���Ă���D��2���ڂ�DFWM��\���Ă���D
�}1��(b)�ɂ����āC�v���[�u���́C�l���g�����ɂ���ăA�C�h�����ɕϊ����ꂽ�Ƃ݂Ȃ���D�}1�ɂ����āC�M�����i�v���[�u���j��1�ł��邪�C�l���g�����𗘗p�����g���ϊ��ł́C�}2�Ɏ����悤�ɕ����̔g���̐M������1�̃|���v���ňꊇ���Ĕg���ϊ������鎖���\�ł���D
�}
2�@���g���ϊ�
3 ���Ȉʑ��ϒ��ƃp���X���k�E�\���g���`��
3.1 ���Ȉʑ��ϒ�
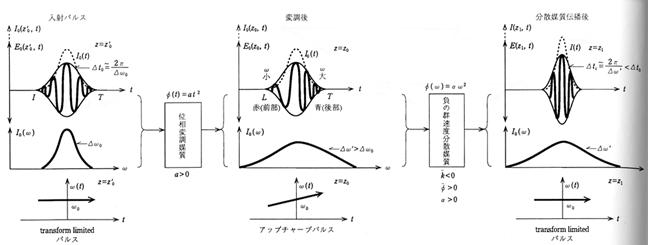
���p���X���C���t�@�C�o�̂悤�Ȍ��J�[���ʌ��ʔ}������`������ƁC�`������z���Z���͈͂ł́C���̈ʑ��ӂ͋��ܗ�n�ƃt�@�C�o�������ɔ�Ⴕ�ĕω�����D�����X�y�N�g���̒��S�ɂ�����g���Ƃ���ƁC
![]() (9)
(9)
�ƕ\�����Ƃ��ł���D�u�����g���́C�ʑ��̔����ł��邩��C�t�@�C�o���̓`������z���Z���C������`�����������͈͂ł́C����`���ɋN��������g���̕ω����́C
![]() (10)
(10)
�ƂȂ�C�p���X�����ԃтɑ��Č����g���������I�ɕω����C���g���`���[�s���O����������D��������Ȉʑ��ϒ��iSPM�j�Ƃ����D�}�ɔ���`�t�@�C�o�ɂ�����C�ߐڂ���2�̃\���g���p���X�̔���`�`���ɔ������g���`���[�s���O�̐��l�v�Z��������D
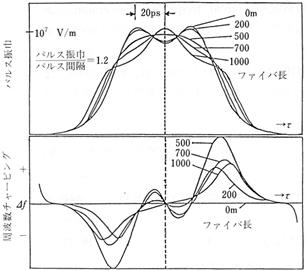
�}
3�@���g���`���[�s���O��L������p���X
3.2 �p���X���k
���`�}���̕��U�������C�p���X���B���ԃсC�`������L�C���g�����������̂Ƃ��C
![]() (11)
(11)
�Ƌߎ�����D
�`���[�s���O��![]() ���O�̐��}���ł�����ƁC�p���X�̑O�ӂł͎��g�����Ⴍ�Ȃ�C�p���X�̌�ӂł͎��g���������Ȃ�C�S�̂Ƃ��ĕ����L�����`�g�ɂȂ�D����
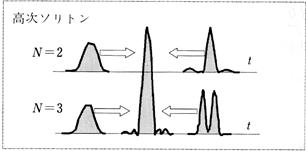
���O�̐��}���ł�����ƁC�p���X�̑O�ӂł͎��g�����Ⴍ�Ȃ�C�p���X�̌�ӂł͎��g���������Ȃ�C�S�̂Ƃ��ĕ����L�����`�g�ɂȂ�D����![]() ���O�̐��`�}���ɁC�`���[�s���O��L����p���X�����̕��`���p���X����˂����ꍇ�́C�`���[�s���O�ɂ����g���V�t�g�����ɑΉ�����Q�x�������ɂ���āC���̕��`�p���X�̌�ӂ́C�O�ӂ�����������D���̌��p���X������L�̐��`���U�}����ʂ�����ŁC���̌�ӂ��O�ӂɒǂ��������ɁC�ŏ��̃p���X����������D��������p���X���k�ƌ����i�}�S�j�D�p���X������0�CL�����̕��U�}�̂̓`�������Ƃ��āC
���O�̐��`�}���ɁC�`���[�s���O��L����p���X�����̕��`���p���X����˂����ꍇ�́C�`���[�s���O�ɂ����g���V�t�g�����ɑΉ�����Q�x�������ɂ���āC���̕��`�p���X�̌�ӂ́C�O�ӂ�����������D���̌��p���X������L�̐��`���U�}����ʂ�����ŁC���̌�ӂ��O�ӂɒǂ��������ɁC�ŏ��̃p���X����������D��������p���X���k�ƌ����i�}�S�j�D�p���X������0�CL�����̕��U�}�̂̓`�������Ƃ��āC
![]() (12)
(12)
�ł���D���ꂩ��C�K�v�ȕ��U�ʂ́C
![]() (13)
(13)
�Ƌ��߂���D
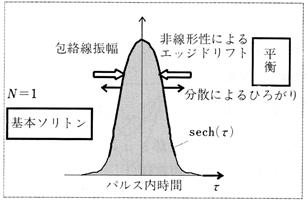
�@���k���ɗp����{�̕��U�}���Ƃ��āC���t�@�C�o�ُ̈핪�U���C���邢�͊��v�C��܊i�q�Ȃǂ��L���铙���I�ȕ����U���g���D���t�@�C�o�Ȃǂ̎��R�̕����U���g�����Ƃ́C���̒l���������C�}���̓����ɂ�肵�悤�g���Ȃǂ����������D���Ċ��v�Ȃǂ́C�p�����[�^�����R�ɐݒ�ł���̂ŁC���p�I�ł���D����Ƃ��Ă͉�܊i�q�𗘗p������̂�C�ӂ��Ԃ�[��y���[��G�^�����Ȃǂ�����D